Minimization Using Myhill - Neurode Theorem

Minimization using Myhill-Neurode Theorem 

To understand the concept of minimization using Myhill-Neurode Theorem, Let us take an example-

  

To Minimize the above DFA using Myhill-Neurode theorem, follow some steps:

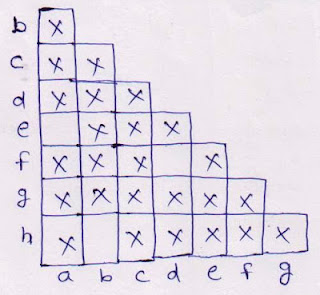
1.> Initially an  X is placed in each entry corresponding to one final state and one non-final state in the following format.

(c,a)  =  X

(c,b)  =  X

(c,d)  =  X

(c,e)  =  X

(c,f)   =  X

(c,g)  =  X

(c,h)  =  X

       

After placing  "X" in the format, then the new format is :

Now take all the blank spaces from the new format like (a,b), (a,d),  (b,d), (a,e), (b,e), (d,e), (a,f), (b,f).....(g,h).

First take (a,b), 

Here for (a,b), we applied input"0" then we got (b,g) and when we applied input"1" then we got (c,f). and Since "X" is already placed correspond to (c,f), so put "X" corresponding to (a,b).

then take (a,d),

Here for (a,d),when we applied input"0" then we got (b,c) and when we applied input"1" then we got (f,g). and Since "X" is already placed correspond to (b,c), so put "X" corresponding to (a,d).

Same process is repeated for , (b,d) and .....(g,h).

then we get the following format:

Here there is no entry corresponding to (a,e) , (b,h) and (d,f). so we combine these states and make a new minimized automata,i,e.,